Đề thi thử đánh giá tư duy Bách khoa có đáp án - Tuyensinh247 (đề 2)

CẤU TRÚC BÀI THI

-----------------------------------------

NỘI DUNG BÀI THI

BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM

PHẦN 1. TƯ DUY TOÁN HỌC

Câu 1. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:

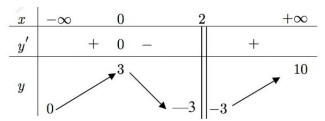
Kéo ô thích hợp thả vào các vị trí để có mệnh đề đúng:

1) Hàm số đã cho có [vị trí 1] điểm cực trị.

2) Hàm số đã cho đạt cực đại tại điểm có hoành độ bằng [vị trí 2].

3) Đồ thị hàm số đã cho có tổng cộng [vị trí 3] đường tiệm cận đứng và ngang.

Câu 2. Số nghiệm của phương trình \({4^{{x^2} - 3x + 2}} + {4^{2{x^2} + 6x + 5}} = {4^{3{x^2} + 3x + 7}} + 1\) là?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 3: Gọi \(M\) là điểm biểu diễn số phức \(z = (2 - i)(3 - 5i)\) và \(N\) là điểm đối xứng của \(M\) qua gốc tọa độ. Điểm \(N\) có hoành độ là ..........

Câu 4. Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(AA'\). Khoảng cách từ điểm \(M\) đến mặt phẳng \((AB'C)\) bằng?

A. \(\dfrac{{a\sqrt 2 }}{4}\).

B. \(\dfrac{{a\sqrt {21} }}{7}\).

C. \(\dfrac{{a\sqrt 2 }}{2}\).

D. \(\dfrac{{a\sqrt {21} }}{{14}}\).

Câu 5. Một chiếc guồng nước có dạng hình tròn bán kính \(2,5m\); trục của nó đặt cách mặt nước \(2m\). Khi guồng quay đều, khoảng cách \(h\) (mét) từ một chiếc gầu gắn tại điểm \(A\) của guồng đến mặt nước được tính theo công thức \(h = |y|\), trong đó:

\(y = 2 + 2,5\sin \left[ {2\pi \left( {t - \dfrac{1}{4}} \right)} \right]\)

với \(t\) (phút) là thời gian quay của guồng. Ta quy ước \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới nước.

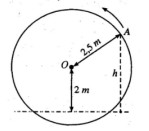
Sau khi guồng nước bắt đầu quay, thời điểm đầu tiên chiếc gầu ở vị trí thấp nhất là .......... phút.

Câu 6. Ba số phân biệt có tổng là \(217\) có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ \(2\), thứ \(9\), thứ \(44\) của một cấp số cộng. Người ta lấy \(n\) số hạng đầu của cấp số cộng này để tổng của chúng bằng \(820\).

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai:

Câu 7. Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {\dfrac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;2} \right]\) bằng \(2\). Số phần tử của tập \(S\) là?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 8. Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu có thể nói được một hoặc hai hoặc ba thứ tiếng: Anh, Pháp hoặc Nga. Biết rằng có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hội nghị cần chọn 1 đại biểu lên phát biểu. Xác suất để chọn được một đại biểu chỉ nói được tiếng Nga là \(\dfrac{a}{{50}}\). Giá trị của \(a\) bằng .............

Câu 9. Cho bình chứa nước được tạo bởi một hình nón không đáy và hình bán cầu, được đặt thẳng đứng trên mặt bàn như hình vẽ:

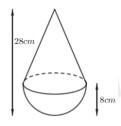
Bình được đổ một lượng nước bằng 70% dung tích của bình. Coi kích thước vỏ bình không đáng kể. 

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

Câu 10. Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{3 - x}}{{\sqrt {x + 1}  - 2}}\,\,\,\,\,khi\,\,\,\,x \ne 3\\mx + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x = 3\end{array} \right.\). Hàm số liên tục tại điểm \(x = 3\) khi \(m\) bằng?

A. \( - 2\)

B. 4

C. \( - 4\)

D. 2

Câu 11. Trong không gian \(Oxyz\) cho mặt phẳng \((P):4y - z + 3 = 0\) và mặt cầu \((S):{(x - 4)^2} + {(y + 4)^2} + {(z - 2)^2} = 4\). Có bao nhiêu điểm \(M\) thuộc mặt phẳng \(Oxy\) với tung độ nguyên, mà từ \(M\) kẻ được tiếp tuyến với \((S)\) đồng thời vuông góc với mặt phẳng \((P)\)?

A. 32

B. 18

C. 34

D. 20

Câu 12. Biết \(F(x)\) và \(G(x)\) là hai nguyên hàm của hàm số \(f(x)\) trên \(\mathbb{R}\) và \(\int\limits_0^5 {f(x){{d}}x}  = F(5) - G(0) + a\,\,(a > 0)\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = F(x),\,\,y = G(x),\,\,x = 0,\,\,x = 5\). Khi \(S = 15\) thì \(a\) bằng ………

Câu 13. Trong không gian \(Oxyz\) cho các vectơ \(\overrightarrow a (1;0; - 2)\), \(\overrightarrow b ( - 1; - 1;3)\) và \(\overrightarrow c (2;3; - 1)\). Gọi giá trị của \(\left( {2\overrightarrow a  - \overrightarrow b } \right)\overrightarrow c \) bằng \(A\). Những mệnh đề nào dưới đây là đúng?

A. \(A\) là số chính phương

B. \(0 < A < 15\)

C. 7 là một ước của \(A\)

D. \(10 < A < 20\)

Câu 14. Cho hàm số \(y = f(x)\) có bảng biến thiên của hàm số \(f'(x)\) như sau:

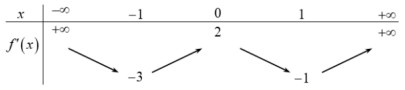
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

Câu 15. Cho \(m\) là số thực. Biết phương trình \({z^2} - 2mz + 9 = 0\) có hai nghiệm phức \({z_1},\,{z_2}\) (có phần ảo khác 0). Có bao nhiêu giá trị nguyên của \(m\) sao cho \({z_1}\left| {\overline {{z_2}} } \right| + {z_2}\left| {\overline {{z_1}} } \right| < 16\)?

A. 3

B. 4

C. 6

D. 5

Câu 16. Số học sinh khối 12 của một trường THPT nằm trong khoảng từ 300 đến 400. Biết rằng nếu xếp tất cả học sinh khối 12 thành các hàng có 5, 8 hoặc 12 người thì có một hàng thiếu 1 em. Số học sinh khối 12 của trường đó là ........... em.

Câu 17. Bé An cần xé giấy màu để dán thành hình chiếc thuyền như sau:

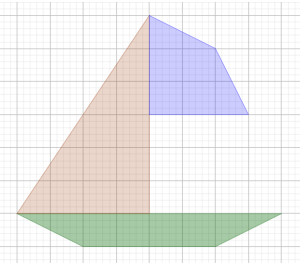
Biết mỗi ô vuông trên giấy có cạnh 1 cm, được chia thành 25 ô vuông nhỏ. 

Diện tích giấy màu bé An cần dùng để dán thành chiếc thuyền là:

A. \(24c{m^2}\)

B. \(18c{m^2}\)

C. \(30c{m^2}\)

D. \(36c{m^2}\)

Câu 18: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là 

\(f(t) = 30{t^2} - {t^3}\),  t=0;1;2;3;…;20

Nếu xem \(f'(t)\) là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\). 

Câu 19. Trong mỗi dung dịch, nồng độ ion \(\left[ {{{{H}}^{{ + }}}} \right]\) đặc trưng cho tính axit. Nếu nồng độ \(\left[ {{{{H}}^{{ + }}}} \right]\) lớn hơn \({10^{ - 7}}\) thì dung dịch có tính axit, nồng độ \(\left[ {{{{H}}^{{ + }}}} \right]\) nhỏ hơn \({10^{ - 7}}\) thì dung dịch có tính kiềm. Vì các nồng độ này là những số rất nhỏ nên để đặc trưng tính axit (tính kiềm) của một dung dịch người ta chỉ xét độ pH, trong đó: \({{pH =  - log}}\left[ {{{{H}}^{{ + }}}} \right]\). Hãy tính nồng độ \(\left[ {{{{H}}^{{ + }}}} \right]\) trong một lon bia, biết lon bia có độ pH là 4,5.

A. 0,0003 

B. 0,003 

C. 0,00003  

D. 0,000003

Câu 20: Cho hàm số \(y = f\left( x \right) = \left| {2x} \right|\). Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

Câu 21: Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}\)?

A. \(y = \dfrac{{2x - 1}}{{x - 1}}\). 

B. \(y = {x^3} + 3x - 1\).

C. \(y = 2{x^4} + 4{x^2}\). 

D. \(y = {x^2} - 2x - 3\).

Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số \(y = \dfrac{{{x^2} + 2mx - 3}}{{x - m}}\) không có cực trị. Số phần tử của tập hợp S là:

A. 0

B. 1

C. 2 

D. 3

Câu 23: Cho bất phương trình \(\left( {m + 2022} \right)\sqrt {4 - {x^2}} {{ \;}} - \sqrt {2 - x} {{ \;}} \le 0\). Tìm m để bất phương trình có nghiệm đúng với mọi x.

A. \(m \le {{ \;}} - \dfrac{{4043}}{2}\)

B. \(m \le \dfrac{{4043}}{2}\)

C. \(m > {{ \;}} - \dfrac{{4043}}{2}\) 

D. \(m \le {{ \;}} - \dfrac{{4041}}{2}\)

Câu 24: Một xe máy đang chạy một thời gian với vận tốc 8 (m/s) thì người lái đạp phanh. Từ thời điểm đạp phanh, xe máy chuyển động chậm dần đều với vận tốc \(v\left( t \right) = {{ \;}} - 3t + 9\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Quãng đường xe máy đi được trong 10 giây cuối cùng là:

A. 60 m.

B. 65 m. 

C. 70 m.  

D. 69,5 m.

Câu 25: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm \(f'\left( x \right)\), có đồ thị \(f\left( x \right)\) như hình sau:

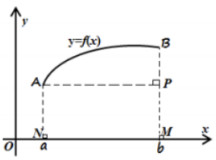
Mệnh đề nào dưới đây đúng?

A. \(\int\limits_a^b {f'\left( x \right)dx} \) là diện tích hình thang ABMN

B. \(\int\limits_a^b {f'\left( x \right)dx} \) là độ dài đoạn BP

C. \(\int\limits_a^b {f'\left( x \right)dx} \) là đồ dài đoạn MN 

D. \(\int\limits_a^b {f'\left( x \right)dx} \) là độ dài đoạn cong AB.

Câu 26: Tìm tất cả các giá trị thực của tham số \(k\) để có \(\int_1^k {(2x - 1)} {{d}}x = 4\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {x + 1}  - 1}}{x}\).

A. \(\left[ {\begin{array}{*{20}{l}}{k = 1}\\{k = 2}\end{array}} \right.\). 

B. \(\left[ {\begin{array}{*{20}{l}}{k = 1}\\{k =  - 2}\end{array}} \right.\).

C. \(\left[ {\begin{array}{*{20}{l}}{k =  - 1}\\{k =  - 2}\end{array}} \right.\). 

D. \(\left[ {\begin{array}{*{20}{l}}{k =  - 1}\\{k = 2}\end{array}} \right.\).

Câu 27: Trong tập số phức, cho dãy \(\left( {{u_n}} \right)\) với \({u_n} = {\left( {i\sqrt 2 } \right)^{n + 1}},\forall n \in {\mathbb{N}^*}\). Mỗi phát biểu sau đây là đúng hay sai?

Câu 28: Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \({u_1} = 4\) và \({u_{n + 1}} = \sqrt {{u_n} + 12} \) với mọi \(n \ge 1\). Số hạng \({u_{10}}\) là ...........

Câu 29: Trên tia \(Ox\) lấy các điểm \({I_1},{I_{_2}},...,{I_n},...\) sao cho với mỗi số nguyên dương n, \(O{I_n} = 2n\). Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia \(Ox\), vẽ các nửa đường tròn đường kính \(O{I_n}\), n=1,2,… Kí hiệu \({u_1}\) là diện tích của nửa hình tròn đường kính \(O{I_1}\) và với mỗi \(n \ge 2\), kí hiệu \({u_n}\) là diện tích của hình giới hạn bởi nửa đường tròn đường kính \(O{I_{n - 1}}\) , nửa đường tròn đường kính \(O{I_n}\) và tia \(Ox\). Khi đó, ta được dãy số \(\left( {{u_n}} \right)\). Khẳng định nào sau đây đúng?

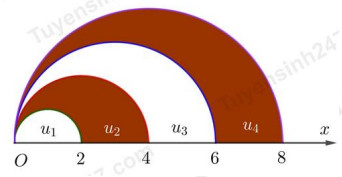
A. \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \(\pi \) 

B. \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \(\dfrac{\pi }{4}\)

C. \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \(\dfrac{\pi }{{16}}\) 

D. \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \(\dfrac{\pi }{2}\)

Câu 30: Một mạng lưới đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó mỗi chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B.

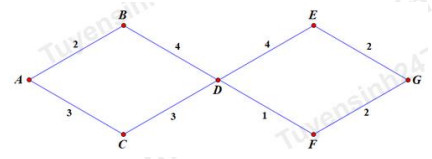
A. 108 

B. 170 

C. 26

D. 82

Câu 31: Kéo thả các đáp án vào chỗ trống:

Giả sử có 12 viên bi khác màu nhau và 3 cái hộp, ta chia đều bi vào các hộp.

Số cách xếp 12 viên vào 3 hộp khác nhau là …………………

Số cách xếp 12 viên vào 3 hộp giống nhau là ………………

Câu 32: Từ khai triển biểu thức \({\left( {x + 1} \right)^{2023}}\) thành đa thức. Tổng các hệ số của đa thức là

A. \({2^{2023}}\) 

B. \(2023\)

C. \({2^{2022}}\) 

D. \(2024\)

Câu 33: Hình hộp đứng ABCD.A’B’C’D’ có đáy là một hình thoi với diện tích \(4c{m^2}\). Hai mặt chéo ACC’A’ và BDD’B’ có diện tích lần lượt bằng \(10c{m^2}\) và \(20c{m^2}\). Thể tích của khối hộp đã cho là

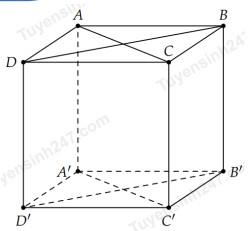
A. \(20c{m^3}\)  

B. \(40c{m^3}\) 

C. \(10\sqrt 2 c{m^3}\) 

D. \(20\sqrt 2 c{m^3}\)

Câu 34: Cho 10 điểm A, B,C, D, E trong đó không có 4 điểm nào đồng phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi 3 trong 10 điểm đã cho?

A. 100

B. 140

C. 120

D. 80

Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng 2a, \(SA = SB = SC = 2a\). Thể tích của khối chóp S.ABCD lớn nhất bằng

A. \(6{a^3}\) 

B. \(2{a^3}\) 

C. \(4{a^3}\)

D. \(12{a^3}\)

Câu 36: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng \(40c{m^2}\) và chu vi bằng \(26cm\). Biết chiều dài của hình chữ nhật lớn hơn bán kính mặt đáy của hình trụ (T). Diện tích toàn phần của hình trụ là:

A. \(\dfrac{{105\pi }}{2}c{m^2}\) 

B. \(65\pi c{m^2}\)

C. \(\dfrac{{105\pi }}{4}c{m^2}\) 

D. \(35\pi c{m^2}\)

Câu 37: Cho hình nón có chiều cao bằng\(2\sqrt 5 \). Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng \(9\sqrt 3 \). Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng

A. \(\dfrac{{32\sqrt 5 \pi }}{3}\). 

B. \(32\pi \) 

C. \(32\sqrt 5 \pi \).

D. \(96\pi \).

Câu 38: Cho hình chóp S.ABCD có đáy là hình thang vuông tại \(A,D,AB = AD = a,{\mkern 1mu} {\mkern 1mu} CD = 2a\). Cạnh bên \(SD \bot \left( {ABCD} \right)\) và \(SD = a\). Gọi \(E\) là trung điểm của DC. Tính bán kính mặt cầu ngoại tiếp hình chóp S.BCE.

A. \(R = \dfrac{{a\sqrt {11} }}{4}\)

B. \(R = \dfrac{{a\sqrt {11} }}{2}\)

C. \(R = \dfrac{{a\sqrt {11} }}{3}\) 

D. \(R = \dfrac{{2a\sqrt {11} }}{{11}}\)

Câu 39: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 1}}{{ - 2}}\) và \({d_2}:\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{2} = \dfrac{{z - 3}}{{ - 2}}.\) Khoảng cách giữa hai đường thẳng này bằng

A. \(\dfrac{{\sqrt {17} }}{{16}}\)

B. \(\dfrac{{\sqrt {17} }}{4}\) 

C. \(\dfrac{{16}}{{\sqrt {17} }}\)

D. 16

Câu 40: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm \(A\left( {3;0;0} \right)\),\(B\left( { - 3;0;0} \right)\) và \(C\left( {0;5;1} \right)\). Gọi \(M\) là một điểm nằm trên mặt phẳng tọa độ \(\left( {Oxy} \right)\) sao cho \(MA + MB = 10\), giá trị nhỏ nhất của MC là

A. \(\sqrt 6 \) .

B. \(\;\sqrt 2 \). 

C. \(\sqrt 3 \).

D. \(\sqrt 5 \).

PHẦN 2. TƯ DUY ĐỌC HIỂU 

Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 10:

VĂN HÓA VIỆT NAM ĐƯƠNG ĐẠI, MỘT GÓC NHÌN - DIỆN MẠO MỚI CỦA VĂN HÓA VIỆT

[0] Công cuộc đổi mới đất nước đến nay đã có một khoảng thời gian gần 30 năm kinh nghiệm để từ đó Đảng, Nhà nước và nhân dân ta nhìn lại tiến trình xây dựng phát triển kinh tế, văn hoá, xã hội. Bước sang TK XXI, đặc biệt là từ năm 2014, đất nước ta bước vào giai đoạn tăng tốc cho sự nghiệp đổi mới, đẩy mạnh công nghiệp hoá, hiện đại hoá và hội nhập quốc tế. Trong bối cảnh đó, diện mạo văn hoá Việt Nam đã có những đổi thay đáng kể.

[1] Những làn sóng giao lưu văn hoá tràn ngập đời sống xã hội

Vừa qua, gương mặt văn hoá Việt Nam đã khởi sắc trong quá trình giao lưu hội nhập văn hoá với quốc tế và khu vực. Không khí khoáng đạt cởi mở của sự nghiệp đổi mới đã tràn ngập trong đời sống văn hoá xã hội Việt Nam. Văn hoá nước ta đã phát triển cả bề rộng và bề sâu trên cơ sở phát huy những giá trị truyền thống, tiếp nhận và biến đổi những tinh hoa văn hoá nhân loại.

Song song với điều đó, nền văn hoá Việt Nam cũng đang tự sản sinh ra những giá trị mới phù hợp với xã hội hiện đại và quá trình toàn cầu hoá đang diễn ra sôi động khắp nơi trên thế giới.

[2] Nếu như trong những thập kỷ 70, 80 của thế kỷ trước, giao lưu văn hoá Xô – Việt chiếm ưu thế tuyệt đối trên mảnh đất văn hoá Việt Nam thì vào những năm cuối TK XX đầu TK XXI, giao lưu văn hoá Việt – Hàn, văn hoá Việt – Trung, văn hoá Việt với văn hoá phương Tây ngày càng sôi động trên phạm vi toàn bộ đời sống văn hoá cả nước. Trong hàng thập kỷ, văn hoá thẩm mỹ, văn hoá nghệ thuật, văn hoá tiêu dùng của Hàn Quốc, Trung Quốc đã tác động rất mạnh đến Việt Nam. Kinh tế hàng hoá Hàn Quốc và Trung Quốc tràn ngập thị trường Việt Nam từ thành thị đến nông thôn, từ miền núi đến hải đảo xa xôi, đâu đâu cũng có thể nhận thấy ảnh hưởng một lối sống tiêu dùng Hàn Quốc.

[3] Hàng hoá của Liên Xô và các nước XHCN Đông Âu trước đây đã trở thành kỷ vật bảo tàng thời bao cấp. Trong lĩnh vực nghệ thuật, giao lưu văn hoá bản địa với văn hoá bên ngoài diễn ra phong phú. Trên thực tế, phim Hàn Quốc đã tiến vào Việt Nam trước một bước để hàng hoá tiêu dùng vào sau, khi đã có được sự quảng cáo rầm rộ, khôn khéo. Hoá mỹ phẩm Hàn Quốc, cách làm đẹp theo kiểu Hàn, chụp ảnh Hàn Quốc, chăn đệm Hàn Quốc, thuốc Đông dược, nhân sâm xứ sở Kim chi tràn ngập thị trường Việt. Các vũ điệu Audition quay tít trên truyền hình lôi cuốn lớp trẻ 8X, 9X. Các thần tượng điện ảnh ca nhạc xứ Hàn lần lượt đến Việt Nam gặp gỡ các fan hâm mộ. Chưa bao giờ mà hoá mỹ phẩm Hàn Quốc lại tràn ngập thị trường Việt Nam như trong thời gian qua. Trên sóng truyền hình, điện ảnh phim Mỹ, Hàn Quốc… chiếm một thời lượng khá lớn và tác động đến thị hiếu thẩm mỹ của đông đảo công chúng trẻ tuổi. Việc du nhập bản quyền các chương trình, vui chơi giải trí nước ngoài như Bước nhảy hoàn vũ, Giọng hát Việt, Nhân tố bí ẩn, Gương mặt thân quen… làm sôi động thị trường văn hoá Việt, nhen nhóm cảm xúc thẩm mỹ cho công chúng hiện đại cũng như những người sản xuất chương trình.

[4] Sự đan cài giữa văn hoá đô thị và văn hoá nông thôn

Bước sang TK XXI, quá trình đô thị hoá diễn ra khắp nơi trên đất nước. Thành phố nhỏ thì quy hoạch lớn hơn để trở thành trung tâm đô thị của một tỉnh. Thị xã thì lên thành phố. Thị tứ thì lên thị trấn. Phố nhỏ thì thành thị tứ. Lối sống đô thị tràn về nông thôn. Người nông thôn bỏ ra đô thị để đô thị hoá thành người thành phố. Người thành phố thì về nông thôn để mua đất xây biệt thự nhà vườn, nhà nghỉ cuối tuần hoặc chờ thời cơ đất lên giá bán, kiếm lợi. Nông thôn biến đổi theo kiểu phố ở trong làng. Còn ở thành thị, những ngôi đình làng trên phố thường bị bao vây bởi vành đai chiếm dụng đất của những người dân xung quanh. Sự cách biệt giữa đô thị và nông thôn thu hẹp dần. Người dân ở những chung cư cao tầng hiện đại vẫn có thói quen nông nghiệp, văn hoá làng quê trong ứng xử. Công tác quản lý đô thị ngày càng khó khăn bởi làn sóng di dân tự do lan rộng. Thành thị trở thành thị trường cho tầng lớp thị dân mới gốc nông thôn, ngày ngày hoà nhập vào dòng người đông đúc đi vào thành phố.

[5] Văn hoá gia đình trước những thách thức mới

Hiện nay, văn hoá gia đình đang đứng trước những thách thức không nhỏ. Trẻ em sinh ra và lớn lên không có nhiều cơ hội gắn bó với cha mẹ như trước đây. Tình trạng cha mẹ đi sớm về khuya, không biết con cái ăn uống và lớn lên như thế nào đang diễn ra phổ biến. Tất cả phó mặc cho nhà trường mầm non hoặc người giúp việc. Tình cảm của con cái đối với cha mẹ đã có những khác biệt. 

XEM TOÀN BỘ ĐỀ