Đề luyện thi đánh giá tư duy Bách khoa - Tư duy Toán học (Đề 1 có đáp án)

 ĐỀ LUYỆN THI ĐÁNH GIÁ TƯ DUY ĐẠI HỌC BÁCH KHOA HÀ NỘI

ĐỀ LUYỆN THI SỐ 1 – PHẦN THI TƯ DUY TOÁN HỌC

THỰC HIỆN: BAN CHUYÊN MÔN TUYENSINH247.COM

NỘI DUNG BÀI THI

TOÁN TRẮC NGHIỆM:

Câu 36: (ID:545189) Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số \[y = \frac{{\left( {{x^2} - 2x} \right)\sqrt {2 - x} }}{{\left( {x - 3} \right)\left[ {{f^2}\left( x \right) + 3f\left( x \right)} \right]}}\] là?

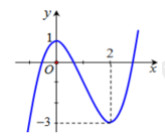
A. 3           B. 4                C. 5            D.  6

Câu 37: (ID:545190) Giả sử \[\int {\frac{{2x + 5}}{{x\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 5} \right) + 9}}dx =  - \frac{1}{{g\left( x \right)}} + C} \]. Tính tổng các nghiệm của phương trình \(g\left( x \right) = 0\).

A. 3          B. –5             C. –3            D.  5

Câu 38: (ID:545191) Tập nghiệm của bất phương trình \[{\log _{\frac{1}{5}}}\frac{{4x + 6}}{x} \ge 0\] là:

A. \[\left( { - 2; - \frac{3}{2}} \right]\]        

B. \[\left[ { - 2; - \frac{3}{2}} \right]\] 

C. \[\left[ { - 2; - \frac{3}{2}} \right)\]       

D.  \[\left( { - 2; - \frac{3}{2}} \right)\]

Câu 39: (ID:545192) Trong không gian Oxyz cho ba đường thẳng \[{d_1}:\frac{{x - 1}}{2} = \frac{{y + 1}}{2} = \frac{{z - 1}}{1},\] \[{d_2}:\frac{x}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z + 1}}{2},\] \[{d_3}:\frac{{x - 3}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{{ - 2}}\]. Mặt phẳng \[\left( P \right):{\rm{ }}ax + by + cz--1 = 0\] với a, b nguyên dương, đi qua M(2;0;1) và cắt 3 đường thẳng trên tại ba điểm là ba đỉnh của một tam giác đều. Hỏi (P) đi qua điểm nào sau đây?

A. (1;3;3)        B. (1;2;3)       C. (2;1;3)       D.  (3;3;1)

Câu 40: (ID:545193) Tứ diện đều ABCD có chiều cao \[h = \sqrt 2 \]. Các trọng tâm của bốn mặt tứ diện tạo thành một tứ diện có thể tích là:

A. \[\frac{{2\sqrt 6 }}{{27}}\]  

B. \[\frac{{\sqrt 6 }}{{108}}\] 

C. \[\frac{{\sqrt 6 }}{{36}}\]       

D.  \[\frac{{2\sqrt 6 }}{9}\]

Câu 41: (ID:545194) Có 6 học sinh gồm 1 học sinh lớp 10, 2 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngẫu nhiên thành một hàng dọc. Xác suất học sinh lớp 10 đứng xen kẽ giữa 2 học sinh lớp 12 là:

A. \[\frac{1}{{10}}\]      B. \[\frac{3}{5}\]       C. \[\frac{1}{5}\]       D.  \[\frac{3}{{10}}\]

Câu 42: (ID:545195) Thể thích khối tròn xoay thu được khi quay một tam giác vuông có cạnh huyền bằng 10 và một cạnh góc vuông bằng 8 quanh chính cạnh góc vuông này là:

A. 96π       B. 124π      C. 128π          D.  140π

Câu 43: (ID:545196) Số giá trị nguyên của hàm số \[y = \frac{{2\sin x - \cos x}}{{\sin x + 2\cos x + 3}}\] là:

A. 1         B. 5           C. 3        D.  Vô số

Câu 44: (ID:545197) Một thợ mộc chế tạo một đồ vật hình trụ từ một khối gỗ hình hộp chữ nhật, có đáy là hình vuông và chiều cao bằng 1,25m bằng cách vẽ hai đường tròn (C) và (C’) nội tiếp hai đáy để tạo ra hai đáy của hình trụ, rồi bỏ đi phần gỗ thừa bên ngoài khối trụ. Biết rằng trong tam giác cong tạo bởi (C) và hình vuông đáy có một hình chữ nhật kích thước 0,3cm x 0,6cm (như hình). Hỏi 10 đồ vật như vậy người thợ mộc sẽ bán được số tiền gần nhất với giá trị nào sau đây, biết giá tiền trung bình của đồ vật tính theo mỗi mét khối là 20 triệu đồng?

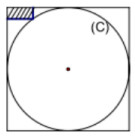
A. 196 nghìn đồng         B. 65 nghìn đồng          C. 176 nghìn đồng         D.  58 nghìn đồng

Câu 45: (ID:545198) Số các số phức thỏa mãn hệ điều kiện \[\left\{ \begin{array}{l}\left| z \right| = 1\\\left| {\frac{z}{{\bar z}} + \frac{{\bar z}}{z}} \right| = \sqrt 3 \end{array} \right.\] là:

A. 1       B. 2           C. 4       D.  8

Câu 46: (ID:545199) Cho hai số phức \[{z_1} = \sqrt 3  + i;{z_2} = \sqrt 3  - i\]. Tìm khẳng định sai:

A. \[{z_1} + {z_2}\] là số thực    

B. \[{z_1} - {z_2}\] là số thuần ảo

C. \[{z_1}.{z_2}\] là số thực    

D.  \[\frac{{{z_1}}}{{{z_2}}}\] là số thuần ảo

Câu 47: (ID:545200) Có bao nhiêu số tự nhiên có 5 chữ số khác nhau với số 4 đứng ở hàng đơn vị được lập từ các chữ số 1, 2, 3, 4, 5?

A. 5         B. 24             C. 120         D.  256

Câu 48: (ID:545201) Cho dãy số (u_n) thỏa mãn \[\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \frac{{n + 1}}{{n + 2}}{u_n} + \frac{3}{{n + 2}}\end{array} \right.,\forall n \in \mathbb{N}*\]. Số hạng thứ 2022 của dãy là:

 A. \[{u_{2022}} = \frac{{2023}}{{2022}}\]   

B. \[{u_{2022}} = \frac{{6065}}{{2023}}\]    

C. \[{u_{2022}} = \frac{{2022}}{{2023}}\]

D.  \[{u_{2022}} = \frac{{607}}{{1213}}\]

Câu 49: (ID:545202) Sự phân rã của một đồng vị phóng xạ được biểu diễn theo công thức \[m\left( t \right) = {m_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\]trong đó m₀ là khối lượng ban đầu của đồng vị phóng xạ (tại thời điểm t = 0); T là chu kỳ bán rã của đồng vị đó. Biết rằng chu kỳ bán rã của đồng vị cacbon 14 (¹⁴C) là khoảng 5730 năm, hỏi một mẫu đồ cổ có độ tuổi là bao nhiêu năm biết rằng trong mẫu đồ cổ này chứa đồng vị cacbon 14 và đồng vị này đã mất khoảng 25% khối lượng ban đầu của nó?

A. 2300 năm          B. 2378 năm        C. 2387 năm         D.  2400 năm

Câu 50: (ID:545203) Một dụng cụ bằng kim loại như hình vẽ, với hai đáy song song được tạo bởi hai hình parabol bằng nhau, hai đáy vuông góc với mặt bên hình chữ nhật. Hình chữ nhật này có chiều rộng 4cm (nằm trên mặt đáy) và chiều dài 6cm. Đỉnh parabol cách hình chữ nhật 3cm. Tính thể tích của dụng cụ?

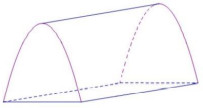
A. 32 cm³          B. 36 cm³         C. 48 cm³           D.  64 cm³

Câu 51: (ID:545204) Cho hình chóp S.ABC có thể tích bằng a³. Mặt (SBC) vuông góc với đáy. Các cạnh \[AB = AC = SA = SB = 2a\]. Cạnh SC bằng:

A. \[a\sqrt 3 \]       B. \[a\sqrt 2 \]       C. \[2a\sqrt 3 \]          D.  \[a\sqrt 6 \]

Câu 52: (ID:545205) Số nghiệm của phương trình \[\frac{{\sin x.\sin 2x + 2\sin x.co{s^2}x + \sin x + \cos x}}{{\sin x + \cos x}} = \sqrt 3 \cos 2x\] trong khoảng \(\left( { - 4;4} \right)\) là:

A. 3         B. 4         C. 5         D.  2

Câu 53: (ID:545206) Có hai người thợ hợp tác cùng chế tạo các đồ thủ công mỹ nghệ. Có hai loại sản phẩm, loại A cần người thợ thứ nhất làm trong 3 giờ và người thợ 2 làm trong 1 giờ, thu lãi 200 nghìn đồng 1 sản phẩm; sản phẩm B cần mỗi người thợ làm trong 1 giờ, thu lãi 160 nghìn đồng 1 sản phẩm. Biết rằng mỗi ngày hai người chỉ có thể làm tối đa lần lượt 6 giờ và 4 giờ. Số tiền lãi có thể thu được nhiều nhất mỗi ngày là:

A. 400 nghìn            B. 720 nghìn         C. 680 nghìn             D.  570 nghìn

Câu 54: (ID:545207) Trong ao có 10 lá sen thẳng hàng, nằm sát mặt nước. Một con ếch đứng ở chiếc lá sen đầu tiên và nó định nhảy đến chiếc lá cuối cùng. Mỗi lần nó có thể nhảy tiến tới tích 1 hoặc 2 bước (tức là không quay lại). Hỏi nó có bao nhiêu cách nhảy để đến đích?

A. 47         B. 51        C. 54        D.  55

Câu 55: (ID:545208) Một đầu bếp cắt một khoanh giò hình trụ theo trục của nó, thì thấy lát cắt có hình vuông có diện tích bằng 9. Giả sử có thể bọc kín khoanh giò này bằng một lớp giấy gói thực phẩm thì diện tích của giấy gói cần dùng vừa đủ là bao nhiêu?

A. 9π          B. 13,5π           C. 4,5π          D.  13π

Câu 56: (ID:545209) Trong không gian Oxyz cho mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = 10\]và hai điểm A(1;2;–4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a + b + c bằng:

A. \[\frac{7}{{41}}\]          B. \[\frac{{23}}{{41}}\]         C. 4             D.  7

Câu 57: (ID:545210) Cho hàm số f(x) liên tục trên \(\mathbb{R}\) thỏa mãn \[\int\limits_{ - 5}^1 {f\left( x \right)dx}  = 9\]. Giá trị của tích phân \[\int\limits_0^2 {\left[ {f\left( {1 - 3x} \right) + 9} \right]} \] là:

A. 75         B. 27      C. 21        D.  15

Câu 58: (ID:545211) Tổng tất cả các nghiệm của phương trình \[{x^3} + 1 = 2\sqrt[3]{{2x - 1}}\] là:

A. 2          B. 1         C. 0           D.  –1

Câu 59: (ID:545212) Cho hai hàm số \[f\left( x \right) = \sqrt[3]{{x\sqrt x }};g\left( x \right) = \sqrt {x\sqrt[3]{x}} \]. Khẳng định nào sau đây đúng:

A. \[f\left( {{2^{2022}}} \right) > g\left( {{2^{2022}}} \right)\]  

B. \[f\left( {{2^{2022}}} \right) < g\left( {{2^{2022}}} \right)\]

C. \[f\left( {{2^{2022}}} \right) = g\left( {{2^{2022}}} \right)\]  

D.  \[f\left( {{2^{2022}}} \right) = 2g\left( {{2^{2022}}} \right)\]

Câu 60: (ID:545213) Tứ diện đều ABCD có cạnh a. Mặt cầu (S) tiếp xúc với AB, AC, AD lần lượt tại B, C, D giới hạn nên một hình cầu có thể tích là:

A. \[\frac{{\pi {a^3}\sqrt 3 }}{2}\]     B. \[\frac{{4\pi {a^3}}}{{81}}\]

C. \[\frac{{\pi {a^3}\sqrt 2 }}{3}\]     D.  \[\frac{{8\pi {a^3}}}{{27}}\]

TOÁN TỰ LUẬN:

Bài 1. (ID:545238)

1. Tìm tất cả các giá trị của m để hàm số \[y = \frac{1}{3}m{x^3} - \left( {m - 1} \right){x^2} + 3\left( {m - 2} \right)x + 2022\] đồng biến trên \[\left[ {2; + \infty } \right)\]

2. Cho dãy số (u_n) có số hạng tổng quát \[{u_n} = 1 - \frac{1}{{{{\left( {n + 1} \right)}^2}}},\forall n \in \mathbb{N}*\]. Tính \[\lim \left( {{u_1}{u_2}...{u_n}} \right)\].

Bài 2. (ID:545241) Một màn hình trong rạp chiếu phim có chiều rộng AB bằng 2,0 mét, đặt cao so với mặt đất một khoảng BH bằng 2,2 mét. C là điểm trên mặt đất có góc nhìn đối với đoạn thẳng AB là lớn nhất. Tính khoảng cách CH từ điểm C tới màn hình.

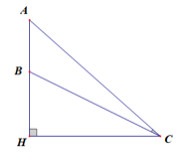
–––––––––––––HẾT–––––––––––––

BẢNG ĐÁP ÁN

Nguồn: Tuyensinh247 - Tổng hợp: Dethidanhgiatuduy.info